PRIMEIRA PROVA DE CÁLCULO NUMÉRICO - 2003
(1º semestre – 12 pontos)
Questão
1-Seja um computador binário, cujo sistema de ponto flutuante tenha 1 bit para o sinal do número, 3 bits para o
expoente e 6 bits para a mantissa num total de 10 bits. (2 pontos)
a- represente, nele, os números r =
2,125 , s = -2,5 , t = 0,55.
b- que número é representado por 1000010100
?
c- qual o maior número positivo
nele representável ?
d- qual o maior número menor que
1 ?
Resolução
Análise
do expoente:
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
-2 |
-2 |
-1 |
0 |
+1 |
+2 |
+3 |
reservado |
a) represente, nele, os
números r = 2,125 ,
s = -2,5 , t = 0,55.
r
= 2,125 = 10,001 = 1,0001
. 21
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
s
= -2,5 = -10,0 = - 1,01 . 21
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
t
= 0,55 = 0,100011001100... =
1,000110011... . 2-1
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
b) que número é representado
por 1000010100 ?
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
-0,0101 . 2-2 = - 0, 000101 = -(
2-4 + 2-6 ) = -0, 078125
c) qual o maior número
positivo nele representável ?
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1,111111 . 23 = 1111,111 = 15,875
d) qual o maior número menor
que 1 ?
1 =
1,0 = 1,000000 . 20
maior número menor que 1 será: 1,111111 . 2-1 =
=
0,1111111 = 1 – 2-7 = 0,9921875
Questão
2-No cálculo da raiz de
f(x) = e -x –
3x –3 = 0 , pelo método da iteração linear, fazem-se as transformações:
·
x = g1(x) = ( e –x –3 ) / 3
·
x = g2(x) = e -x
- 2x – 3
·
x = g3(x) = - ln(3+3x)
Obtenha,
graficamente, uma boa estimativa xo ,
da raiz. (1 ponto)
Indique,
sem iteragir, que função ou funções irão convergir para a raiz. (1 ponto)
Resolução
Como
vemos, fazendo e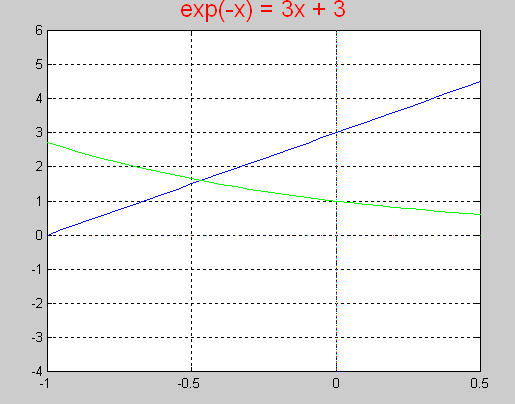
-x = 3x + 3, temos que x0 = - 0,5 é uma
boa estimativa para a raiz.
Para
ver quais funções convergiriam para a raiz, tem-se que calcular as derivadas.
g1’(x) = - e –x
/ 3 onde g1’(-0,5)
= -0,55 que
estando entre (-1,+1) garante a convergência.
g2’(x) = -e -x
– 2 onde g2’(-0,5)
= -3,65 não convergindo
g3’(x) = -
3/(3+3x) onde g3’(-0,5)
= -2 não convergindo.
Logo, só podemos garantir a convergência da função g1(x).
Questão
3-Pelo método de Newton-Raphson, calcule a raiz positiva da equação
f(x)
= e x – 2cos(x) = 0, com erro menor que 0.001. (1 ponto)
Resolução
Vamos
estimar graficamente a raiz, fazendo ex = 2 cos(x).
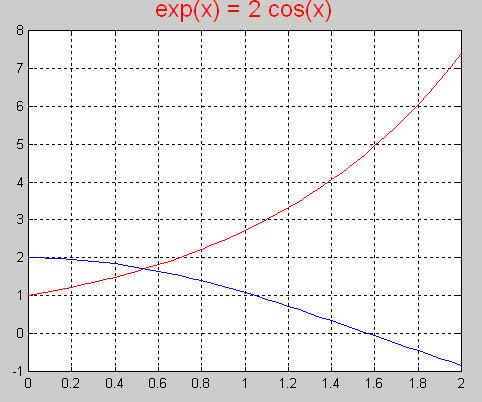
Vê-se que a raiz é aproximadamente 0,5. Logo x0
= 0,5.
Sendo
f(x) = e x – 2cos(x), tem-se f’(x) = e x
+ 2sen(x).
Fazendo-se
xi+1 = xi – f(xi)/f’(xi+1)
tem-se:
xi+1 = xi – (e xi – 2cos(xi
)/( exi + 2sen(x)).
Daí
a seqüência:
x0 = 0,5 x1 = 0,54082 com Dx
= 0,04082 > 0,001
x1= 0,54082 x2 = 0,53979 com Dx
= 0,00103 > 0,001
x2 = 0,53979 x3 = 0,53979 com Dx = 0 < 0,001.
Logo r @ 0,53979 ou r @ 0,540.
Questão
4-Resolva o sistema A.X = B , abaixo, pelo método iterativo de Gauss Seidel, fazendo neste três iterações completas,
partindo de (0,0,0) e usando 2 casas decimais. (1
ponto)
5 X1
- 2 X2 = 1,0
-1 X1 + 5 X2 – 1 X3 =
10,0
- 2 X2 + 5 X3 =
-9,0
Resolução
Método de Gauss-Seidel
x1 = (1,0 + 2 x2) / 5
x2
= (10,0 + x1 + x3)
/ 5
x3 = (-9,0 +
2x2) / 5
Seqüência de iterações:

Raízes:
x1 = 1,00 x2 =
2,00 x3 = -1,00
Questão
5- Resolva a questão anterior pelo método LU. (1 ponto)
Resolução

Ao
se fazer L2 – (-1/5) L1 , isto
é: L2 + (1/5) L1
tem-se:
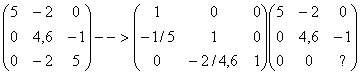
Ao
se fazer L3 – (-2/4,6)L2 , isto
é: L3 + (2/4,6) L2 tem-se:
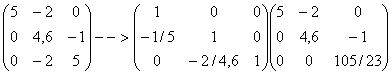
ou:

A =
L . U
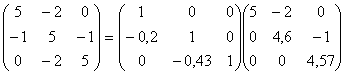
A .
X = B L . U . X = B fazendo
U . X = Y , tem-se:
L .
Y = B que é um sistema triangular de
fácil solução.

Logo: Y1 = 1 -0,2
+ Y2 = 10 logo Y2 = 10,2
-0,43 . 10,2 + Y3 = -9 logo Y3 = -4,61

Mas U.X = Y , logo:

Assim:
X3
= -1,01
4,6 X2 + 1,01 = 10,2 donde X2
= 2,00
5X1 – 4 = 1 donde X1 = 1,00
Assim:

Questão
6-Calcule, com erro menor que 0,1 , as 3 raízes
do polinômio abaixo, por Birge-Vieta.
Trabalhe com 2 casas decimais. (1,5 pontos)
P(x) = 1,0 x3
– 14 x2 + 35 x
+ 50 = 0
Resolução x0 = 0
|
|
1 |
-14 |
35 |
50 |
|
0 |
1 |
-14 |
35 |
50 |
|
0 |
1 |
-14 |
35 |
|
x1 = 0 – 50/35 = -1,43
|
|
1 |
-14 |
35 |
50 |
|
-1,43 |
1 |
-15,43 |
57,06 |
-31,60 |
|
-1,43 |
1 |
-16,86 |
81,17 |
|
x2 = -1,43 – (-31,60)/81,17 = -1,04
|
|
1 |
-14 |
35 |
50 |
|
-1,04 |
1 |
-15,04 |
50,64 |
-2,67 |
|
-1,04 |
1 |
-16,08 |
67,36 |
|
x3 = -1,04 – (-2,67)/67,36 = -1,00
|
|
1 |
-14 |
35 |
50 |
|
-1,00 |
1 |
-15 |
50 |
0 |
r1 = -1,00
x0= -1,00
|
|
1 |
-15 |
50 |
|
-1,00 |
1 |
-16 |
66 |
|
-1,00 |
1 |
-17 |
|
x1 = -1,00 – 66/(-17)= 2,88
|
|
1 |
-15 |
50 |
|
2,88 |
1 |
-12,12 |
15,09 |
|
2,88 |
1 |
-9,24 |
|
x2 = 2,88 –
15,09/(-9,24)= 4,51
|
|
1 |
-15 |
50 |
|
4,51 |
1 |
-10,49 |
2,69 |
|
4,51 |
1 |
-5,98 |
|
x3 = 4,51 – 2,69/(-5,98) = 4,96
|
|
1 |
-15 |
50 |
|
4,96 |
1 |
-10,04 |
0,20 |
|
4,96 |
1 |
-5,08 |
|
x4 = 4,96 – 0,20/(-5,08) = 5,00
|
|
1 |
-15 |
50 |
|
5,00 |
1 |
-10 |
0 |
r2 = 5,00
x0 = 5,00
|
|
1 |
-10 |
|
5,00 |
1 |
-5 |
|
5,00 |
1 |
|
x1 = 5,00 –(-5/1) = 10,00
|
|
1 |
-10 |
|
10,00 |
1 |
0 |
r3 = 10,00
Raízes:
-1,00 5,00 10,00
Questão 7 – O que entende por matriz mal condicionada? Que cuidados devem ser tomados quando aparecem em sistemas lineares. (0,5 ponto) O que entende por convergência linear e convergência quadrática, no cálculo de raízes ?(0,5 ponto) Explique a importância do Método LU.(0,5 ponto)
Resolução
Entende-se por Matriz Mal
Condicionada a matriz cujo determinante é muito pequeno quando comparado
com a ordem de grandeza de seus elementos. (uma definição mais precisa exigiria
definir norma de matriz). São matrizes que, quando envolvidas na solução de
sistemas lineares, tornam os resultados pouco confiáveis, pois pequenos
arredondamentos nos componentes da matriz, ou em resultados intermediários,
alteram profundamente o cálculo final das raízes do sistema. Tendo um Sistema
Linear uma matriz mal condicionada, os cálculos deverão ser feitos com a maior
precisão possível, procurando-se minimizar a propagação desses erros, que são
críticos nesse caso, podendo levar a resultados profundamente diferentes dos
verdadeiros.
Convergência– quando se calcula uma raiz de uma equação por um processo iterativo, busca-se,
a cada nova iteração, aproximar-se mais e mais do verdadeiro valor da raiz. Em
cada iteração, entretanto, há um erro associado a ela. Num método que convirja,
a tendência é a da diminuição dos erros, que deverão tender a zero.
Se o erro de uma iteração é aproximadamente
proporcional ao erro da iteração anterior, isto é, ei+1 » k.ei , diz que a convergência é
linear, sendo |k| < 1.
Se
ei+1 » k ei2
, isto é, se cada novo erro é proporcional ao quadrado do erro anterior,
diz-se que a convergência é quadrática.
Admitindo-se
que os erros sejam pequenos, o quadrado do erro tende a zero mais rapidamente,
daí a convergência quadrática ser mais rápida que a convergência linear.
Método
LU para
resolução de Sistemas Lineares– nesse método,
fatora-se a matriz do sistema no produto de duas matrizes: uma triangular
inferior e outra triangular superior. Assim, transforma-se um sistema A.X = B num sistema L.U.X = B, onde L é uma matriz
triangular inferior e U uma matriz triangular superior.
Chamando-se
U.X de Y , tem-se o sistema L.Y = B, de imediata
solução, pois L é uma matriz triangular.
Calculado
o vetor Y, passa-se ao sistema U.X = Y, também
triangular e de solução imediata.
Assim
calcula-se X, que é a solução do sistema A.X = B.
É
muito comum, na prática, ter-se que resolver sistemas onde só muda o vetor B,
considerado, em geral, a carga do sistema. A solução fica acelerada pela
fatoração inicial da matriz A e a resolução posterior de dois sistemas
triangulares. Para cada
novo vetor B, lado direito do sistema, repete-se a solução dos dois sistemas
triangulares, de solução rápida.